I. Các kiến thức cần nhớ
1. Số hữu tỉ
Số hữu tỉ là số viết được dưới dạng phân số \(\frac{a}{b}\) với \(a,b \in \mathbb{Z},\,b \ne 0.\)
Tập hợp số hữu tỉ được kí hiệu là \(\mathbb{Q}\).
Ví dụ: \(\frac{1}{2};\,3…\) là các số hữu tỉ.
2. Biểu diễn số hữu tỉ trên trục số
+ Ta có thể biểu diễn mọi số thực hữu tỉ trên trục số. Trên trục số, điểm biểu diễn số hữu tỉ $x$ được gọi là điểm $x$ .
Ví dụ:
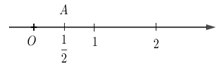
Số hữu tỉ \(\frac{1}{2}\) được biểu diễn bởi điểm \(A\) nằm bên phải điểm \(0\) (như hình vẽ).
So sánh hai số hữu tỉ
+ Với hai số hữu tỉ bất kì $x,y$ ta tuôn có hoặc \(x = y\) hoặc \(x < y\) hoặc \(x > y\).
+ Nếu \(x < y\) thì trên trục số $x$ ở bên trái điểm $y$, nếu \(x > y\) thì trên trục số \(x\) ở bên phải điểm \(y\).
+ Số hữu tỉ lớn hơn $0$ được gọi là số hữu tỉ dương
+ Số hữu tỉ nhỏ hơn $0$ được gọi là số hữu tỉ âm
+ Số hữu tỉ $0$ không là số hữu tỉ dương cũng không là số hữu tỉ âm.
II. Các dạng toán thường gặp
Dạng 1: Biểu diễn số hữu tỉ trên trục số
Phương pháp:
+) Nếu \(\frac{a}{b}\) là số hữu tỉ dương, ta chia khoảng có độ dài 1 đơn vị làm $b$ phần bằng nhau, rồi lấy về phía chiều dương trục $Ox$ là $a$ phần , ta được vị trí của số \(\frac{a}{b}\).
+) Nếu \(\frac{a}{b}\) là số hữu tỉ âm, ta chia khoảng có độ dài $1$ đơn vị làm $b$ phần bằng nhau, rồi lấy về phía chiều âm trục $Ox$ là $a$ phần , ta được vị trí của số \(\frac{a}{b}\).
Dạng 2: So sánh hai số hữu tỉ
Phương pháp:
Để so sánh hai số hữu tỉ ta thường đưa chúng về các phân số có cùng mẫu số dương rồi so sánh tử số với nhau.
* Đưa về các phân số có cùng mẫu số dương rồi so sánh tử số.
* So sánh với số $0$ , so sánh với số $1$ , với $ – 1$ …
* Dựa vào phần bù với $1$; …
* So sánh với phân số trung gian ( là phân số có tử số của phân số này mẫu số của phân số kia)