1. Hệ thức về cạnh và đường cao trong tam giác vuông
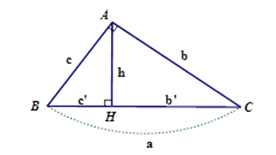
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$. Khi đó ta có các hệ thức sau:
+) $A{B^2} = BH.BC$ hay ${c^2} = a.c’$
+) $A{C^2} = CH.BC$ hay ${b^2} = ab’$
+) $AB.AC = BC.AH$ hay $cb = ah$
+) $H{A^2} = HB.HC$ hay ${h^2} = c’b’$
+) $\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}}$ hay $\frac{1}{{{h^2}}} = \frac{1}{{{c^2}}} + \frac{1}{{{b^2}}}$.
+) $B{C^2} = A{B^2} + A{C^2}$ (Định lí Pitago).
2. Tỉ số lượng giác của góc nhọn
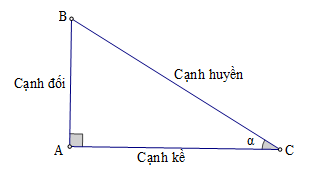
Các tỉ số lượng giác của góc nhọn \(\alpha \) (hình) được định nghĩa như sau:
\(\sin \alpha = \frac{{AB}}{{BC}};\cos \alpha = \frac{{AC}}{{BC}};\tan \alpha = \frac{{AB}}{{AC}};\cot \alpha = \frac{{AC}}{{AB}}\)
+ Nếu \(\alpha \) là một góc nhọn bất kỳ thì
\(0 < \sin \alpha < 1;0 < \cos \alpha < 1\), \(\tan \alpha > 0;\cot \alpha > 0\) , \({\sin ^2}\alpha + {\cos ^2}\alpha = 1;\tan \alpha .\cot \alpha = 1\)
$\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};$$\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }};$
$1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }};$$1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}$
Chú ý: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Với hai góc \(\alpha ,\beta \) mà \(\alpha + \beta = {90^0}\),
Ta có: \(\sin \alpha = \cos \beta ;\cos \alpha = \sin \beta ;\tan \alpha = \cot \beta ;\cot \alpha = \tan \beta. \)
Nếu hai góc nhọn \(\alpha \) và \(\beta \) có \(\sin \alpha = \sin \beta \) hoặc \(\cos \alpha = \cos \beta \) thì \(\alpha = \beta \)
So sánh các tỉ số lượng giác
Với \(\alpha ;\beta \) là hai góc nhọn bất kì và \(\alpha < \beta \) thì
\(\sin \alpha < \sin \beta ;\,\cos \alpha > \cos \beta ;\tan \alpha < \tan \beta ;\cot \alpha > \cot \beta .\)
3. Bảng tỉ số lượng giác các góc đặc biệt
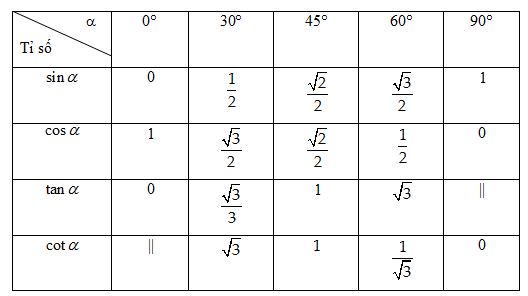
4. Hệ thức về cạnh và góc trong tam giác vuông
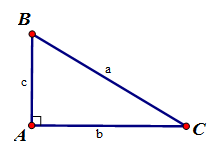
Trong một tam giác vuông
+) Cạnh góc vuông = (cạnh huyền ) x (sin góc đối) = (cạnh huyền ) x (cosin góc kề)
+) Cạnh góc vuông = (cạnh góc vuông ) x (tan góc đối) = (cạnh góc vuông còn lại ) x (cotan góc kề).