I. Các kiến thức cần nhớ
1. Định nghĩa đường tròn
Đường tròn tâm $O,$ bán kính $R$ là hình gồm các điểm cách $O$ một khoảng bằng $R,$ kí hiệu $\left( {O;R} \right)$.
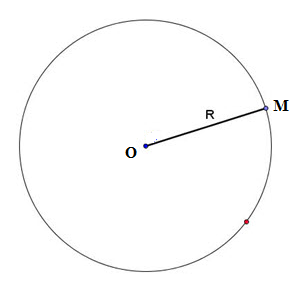
Chú ý:
– Với mọi điểm $M$ nằm trong mặt phẳng thì:
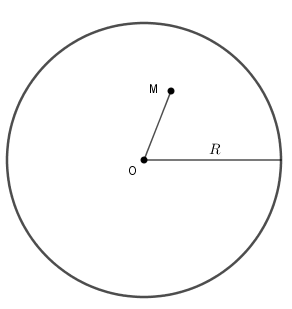
+ Nếu $OM < R$ thì điểm $M$ nằm trong đường tròn $\left( {O;R} \right)$
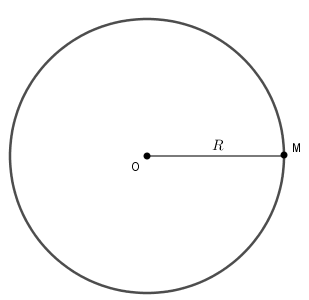
+ Nếu $OM = R$ thì điểm $M$ nằm trên (thuộc) đường tròn $\left( {O;R} \right)$.
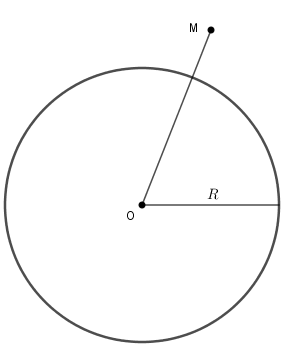
+ Nếu $OM > R$ thì điểm $M$ nằm ngoài đường tròn $\left( {O;R} \right)$.
2. Định nghĩa hình tròn
Hình tròn là hình gồm các điểm nằm trên đường tròn và các điểm nằm bên trong đường tròn đó.
3. Cung, dây cung, đường kính
+ Hai điểm $A,B$ nằm trên đường tròn chia đường tròn thành hai phần, mỗi phần gọi là một cung tròn (cung). Hai điểm $A,B$ là hai mút của cung.
+ Đoạn thẳng $AB$ gọi là một dây cung.
+ Dây cung đi qua tâm là đường kính.
– Đường kính dài gấp đôi bán kính và là dây cung lớn nhất.
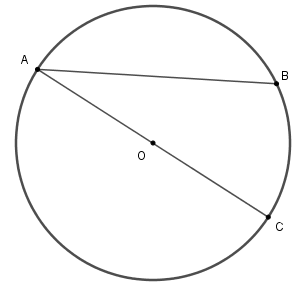
Với hình vẽ trên thì đoạn thẳng $AB$ là dây cung và đoạn thẳng $AC$ là đường kính.
Khi đó $AC \ge AB.$
II. Các dạng toán thường gặp
Dạng 1: Nhận biết vị trí một điểm đối với đường tròn
Phương pháp:
– Với mọi điểm $M$ và $\left( {O;R} \right)$ nằm trong mặt phẳng thì:
+ Nếu $OM < R$ thì điểm $M$ nằm trong đường tròn $\left( {O;R} \right)$
+ Nếu $OM = R$ thì điểm $M$ nằm trên (thuộc) đường tròn $\left( {O;R} \right)$.
+ Nếu $OM > R$ thì điểm $M$ nằm ngoài đường tròn $\left( {O;R} \right)$.
Dạng 2: Đếm số dây cung, số cung của đường tròn
Phương pháp:
+ Đoạn thẳng nối hai điểm phân biệt trên đường tròn tạo thành một dây cung. Hai điểm này chia đường tròn chia đường tròn thành hai phần, mỗi phần gọi là một cung tròn (cung).
+ Trên đường tròn cho $n\,\left( {n \ge 2} \right)$ điểm phân biệt. Nối mỗi cặp điểm ta được một dây cung thì số dây cung tạo thành là $\frac{{n\left( {n – 1} \right)}}{2}$ và số cung tạo thành là $n\left( {n – 1} \right)$.